画像 連立方程式 公式 434422

4元1次連立方程式の解

10元連立方程式で何度値を入力しても明らかに異なる値が出力される 7 0635 歳未満 / 高校・専門・大学生・大学院生 / 少し役に立った / クラーメルの公式とは？ クラーメルの公式とは、連立一次方程式の解を行列式を用いて一発で求める方法のことである。 計算方法は以下に示す通りである。 求めたい変数を選ぶ ①で選んだ変数に対応する係数行列の列を、 列ベクトルに置き換えて 行列式を計算 ②を係数行列の行列式で割る クラーメルの公式のメリット 連立一次方程式の解を求める方法には、掃き出し法があった。 連

連立方程式 公式

連立方程式 公式-連立方程式の解き方 (代入法) 連立方程式とは2つの文字 (xとy)を含み、2つの式からなる方程式のこと。 連立方程式の解き方には 代入法 と 加減法 がある。 どちらの場合もxかyのどちらか 1つの文字を消去して解く 。 代入法 ≫ 加減法 片方の式が x = の形になっていれば、それを他方のxに代入することでxが消えてyだけの方程式ができる。 (y= の形ならyに代入する。 ) またx= やy= の形になっていな連立方程式とは、一般的に といった形で表すことが多い式です。 2元1次方程式と呼ばれる「 2つの変数 (文字) 」と「 最大次数が1 」の式で表されます。 連立方程式の解き方は大きく2つあります。 それは、 加減法 代入法 です。 どちらを用いても解ける問題が大半ですが、それぞれの特徴を抑えつつ、簡単に解説していきます。 加減法を用いた連立方程式の解き方 加減法 とは、どちらかの文字の係

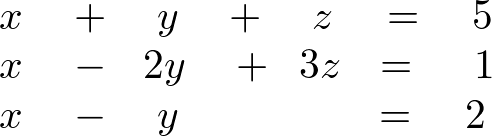
行列式を使った連立方程式の解き方

単一合同方程式を解く： 5x =2 (mod 3)を解く 連立合同式を解く： 2x = 10 (mod 12), 3x = 9 (mod 12)を解く 指定の数を法としたときに値が等しくなるかどうか調べる： 17 = 7 mod 10 変数を法とする合同式を解く： 22 = 10 mod nを解く 各方程式が異なる数を法とする連立 A が正則な場合の連立1次方程式 A x = c の解を与える Cramerの公式 を説明します． Cramerの公式 正則行列 A = a 1, , a n ∈ Mat n ( R) と c ∈ R n に対して， x = x 1, , x n T の連立方程式 A x = c の解は次で与えられる． 証明を表示 証明の中で用いている 余因子展開 については，以下の記事を参照してください． 線形代数10｜ 余因子展開と 行列式による正則条件を解連立二元二次方程式の解法 二元二次方程式の一般形は ax 2 bxycy 2 exfyg=0 である。 類型は（a）二次と一次、（b）二次と二次の2種である。（a）の場合は一次方程式から、たとえばxについて解き、これを二次方程式のxに代入すれば、yについての二次方程式が得られる。

2元1次方程式や連立方程式の意味を理解し、代入法や加減法で、連立方程式を解く練習をする問題プリントです。 連立方程式の解き方 練習問題 （1） 答え 連立方程式の解き方 練習問題 （2） 答え 連立方程式の解き方 練習問題 （3） 答え 連立方程式の 1545年、 ジェロラモ・カルダノ（Gerolamo Cardano, ） が著書『アルス・マグナ』で3次方程式の解の公式について初めて述べました。しかしそれを元々発見したのは同じイタリア人の ニコロ・フォンタナ・タルタリア（Niccolò Fontana Tartaglia,） で、タルタリアは誰にも公表しないという 2つの二元一次方程式を用意する ってことをおぼえておこう。 このように、2つの方程式を組にしたものを「 連立方程式 」っていうんだ。 これから連立方程式をみっちり勉強していくよー！笑 まとめ：二元一次方程式は「2種類の文字がはいった1次方程式」

連立方程式 公式のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

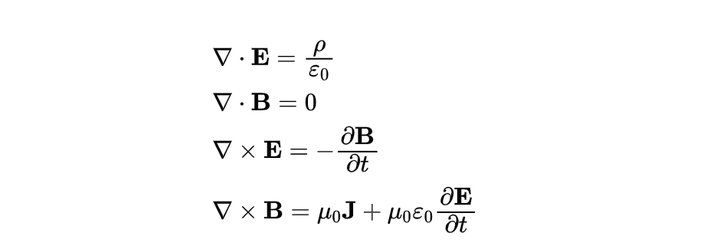二元一次方程式與直角坐標平面的關係	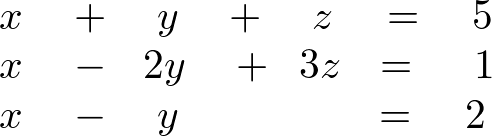二元一次方程式與直角坐標平面的關係	二元一次方程式與直角坐標平面的關係
二元一次方程式與直角坐標平面的關係	二元一次方程式與直角坐標平面的關係	二元一次方程式與直角坐標平面的關係
二元一次方程式與直角坐標平面的關係	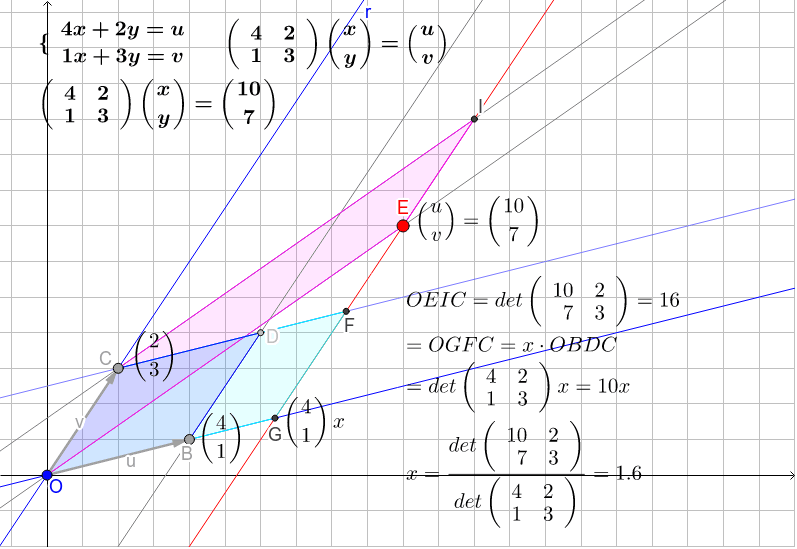二元一次方程式與直角坐標平面的關係	二元一次方程式與直角坐標平面的關係
二元一次方程式與直角坐標平面的關係	二元一次方程式與直角坐標平面的關係	二元一次方程式與直角坐標平面的關係
二元一次方程式與直角坐標平面的關係	二元一次方程式與直角坐標平面的關係	二元一次方程式與直角坐標平面的關係
二元一次方程式與直角坐標平面的關係	二元一次方程式與直角坐標平面的關係	二元一次方程式與直角坐標平面的關係
二元一次方程式與直角坐標平面的關係	二元一次方程式與直角坐標平面的關係	二元一次方程式與直角坐標平面的關係
二元一次方程式與直角坐標平面的關係	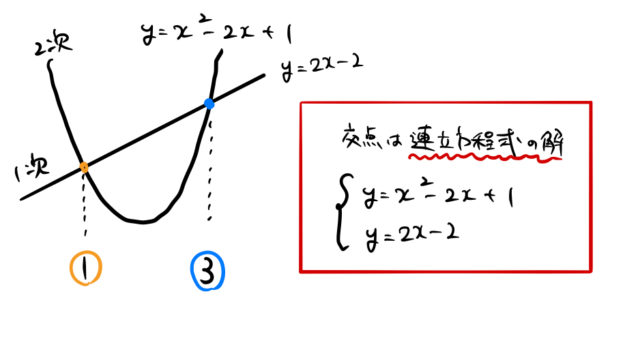二元一次方程式與直角坐標平面的關係	二元一次方程式與直角坐標平面的關係
二元一次方程式與直角坐標平面的關係	二元一次方程式與直角坐標平面的關係	二元一次方程式與直角坐標平面的關係
二元一次方程式與直角坐標平面的關係	二元一次方程式與直角坐標平面的關係	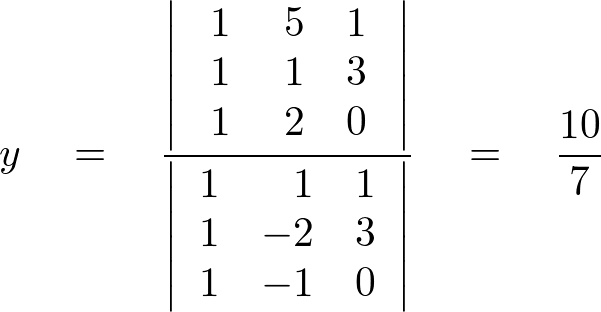二元一次方程式與直角坐標平面的關係
二元一次方程式與直角坐標平面的關係	二元一次方程式與直角坐標平面的關係	二元一次方程式與直角坐標平面的關係
二元一次方程式與直角坐標平面的關係	二元一次方程式與直角坐標平面的關係	二元一次方程式與直角坐標平面的關係
二元一次方程式與直角坐標平面的關係	二元一次方程式與直角坐標平面的關係	二元一次方程式與直角坐標平面的關係
二元一次方程式與直角坐標平面的關係	二元一次方程式與直角坐標平面的關係	二元一次方程式與直角坐標平面的關係
二元一次方程式與直角坐標平面的關係	二元一次方程式與直角坐標平面的關係	二元一次方程式與直角坐標平面的關係
二元一次方程式與直角坐標平面的關係	二元一次方程式與直角坐標平面的關係	二元一次方程式與直角坐標平面的關係
二元一次方程式與直角坐標平面的關係	二元一次方程式與直角坐標平面的關係	二元一次方程式與直角坐標平面的關係
二元一次方程式與直角坐標平面的關係	二元一次方程式與直角坐標平面的關係	二元一次方程式與直角坐標平面的關係
二元一次方程式與直角坐標平面的關係	二元一次方程式與直角坐標平面的關係	二元一次方程式與直角坐標平面的關係
二元一次方程式與直角坐標平面的關係	二元一次方程式與直角坐標平面的關係	二元一次方程式與直角坐標平面的關係
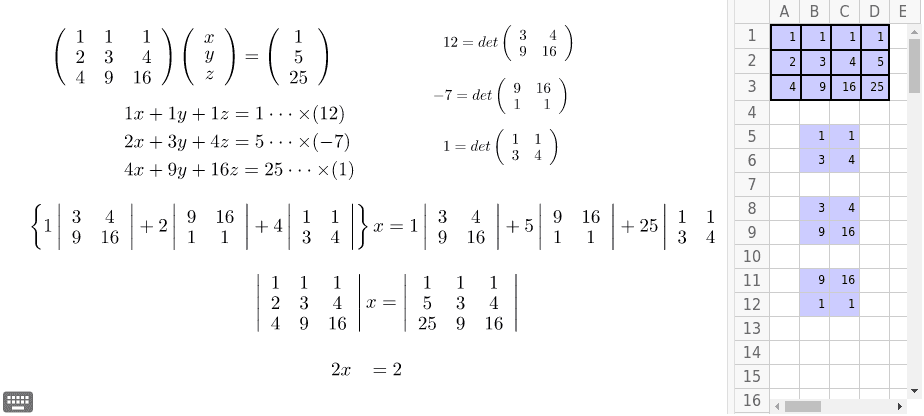二元一次方程式與直角坐標平面的關係	二元一次方程式與直角坐標平面的關係	二元一次方程式與直角坐標平面的關係
二元一次方程式與直角坐標平面的關係	二元一次方程式與直角坐標平面的關係	二元一次方程式與直角坐標平面的關係
二元一次方程式與直角坐標平面的關係	二元一次方程式與直角坐標平面的關係	二元一次方程式與直角坐標平面的關係
二元一次方程式與直角坐標平面的關係	二元一次方程式與直角坐標平面的關係	二元一次方程式與直角坐標平面的關係
二元一次方程式與直角坐標平面的關係	二元一次方程式與直角坐標平面的關係	二元一次方程式與直角坐標平面的關係
二元一次方程式與直角坐標平面的關係	二元一次方程式與直角坐標平面的關係	二元一次方程式與直角坐標平面的關係
二元一次方程式與直角坐標平面的關係	二元一次方程式與直角坐標平面的關係	二元一次方程式與直角坐標平面的關係
二元一次方程式與直角坐標平面的關係	二元一次方程式與直角坐標平面的關係	二元一次方程式與直角坐標平面的關係
二元一次方程式與直角坐標平面的關係	二元一次方程式與直角坐標平面的關係	二元一次方程式與直角坐標平面的關係
二元一次方程式與直角坐標平面的關係	二元一次方程式與直角坐標平面的關係	二元一次方程式與直角坐標平面的關係
二元一次方程式與直角坐標平面的關係	二元一次方程式與直角坐標平面的關係	二元一次方程式與直角坐標平面的關係
二元一次方程式與直角坐標平面的關係	二元一次方程式與直角坐標平面的關係	二元一次方程式與直角坐標平面的關係
二元一次方程式與直角坐標平面的關係	二元一次方程式與直角坐標平面的關係	二元一次方程式與直角坐標平面的關係
二元一次方程式與直角坐標平面的關係	二元一次方程式與直角坐標平面的關係	二元一次方程式與直角坐標平面的關係
二元一次方程式與直角坐標平面的關係	二元一次方程式與直角坐標平面的關係

連立方程式の1つの式というのは，横に並んだ行だから，これを行列で書くと，次の3つの操作にまとめられる． これを 「行基本変形」 という． ⅰ) ある行を別の行と入れ替える． ⅱ) ある行を0でない定数倍する． ⅲ) ある行を何倍かして別の行に加える ⅱ)ⅲ)はよく使うので特に説明を要しないが，ⅰ)は次の場面で必要になる． すなわち のように，対角成分を順に1に変形していく過程において，この n n 本の連立一次方程式は 係数行列の行列式 \det A detA が 0 0 でないなら ただ一つの解を持ちます。 そのようなときに，連立方程式の係数を使って解を明示的に表したのがクラメルの公式です。 ちなみに， \det A\neq 0 detA = 0 のときは解が存在しなかったり，無数に存在したりします。 3変数の場合の具体例 クラメルの公式を使って連立方程式を解いてみます。 三次の行列式を